字典树

2016-04-29

昨天数据结构作业综合题正好遇见了一道题目，一眼看过去感觉是一道字典树裸题，随便就水过去了。正好早上没事情做，更新记录一篇字典树。

概述：

字典树，Trie树。这种树形结构用于统计，排序，保存大量字符串但不仅限于字符串。其优点在于，这种存储方式利用字符串公共前缀来减少查找时间，效率极高。

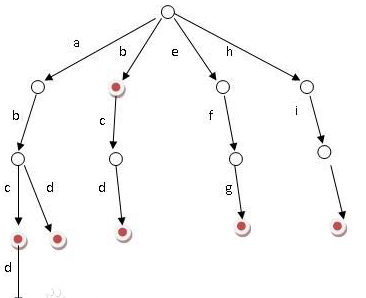
定义：

字典树的结点分为两个域，一个是指针域，来表达其儿子结点所代表的字符，另一个是变量num的int域，用来存储到从根节点到这儿子结点为止，所组成的字符串，作为字符串前缀，有多少字符串拥有这个前缀。
字典树的根节点是一个空节点，他的num值永远为0.
字典树的指针域为一个指针数组，其长度为26从pnext[0]~pnext[25]分别代表’a’~’z’(当然你也可以根据你的字符串形式来改变你的指针数组长度以及其代表意义，这里我们以小写字母为例)。

struct Node{
    Node *next [26];
      int num;
};

假设从根节点开始插入一个字符’a’，那么便创造一个新节点，并将根节点的next[0]指向这个节点。

Node t = Create();
head.next[0]=t;

若是从根节点开始插入一个字符’b’，那么就是讲根节点的next[1]指向一个新的节点。从这可以看出，字典树的节点在存储字符形式中，它并不是显式的直接保存这个字符信息，而是将这个字符与指针域做出一个映射关系，假若某个节点的第X个指针为非空指针，其指向一个节点，则说明这个第X个指针所对应的字符串被存储在这条路径中。

从上可以看出，字典树的构造操作十分简单，仅仅分为创造节点与插入节点

创造节点

每次创造节点以后记得将节点的域初始化。

Node* Creat(){
Node* p =new Node();
for(int i=0;i<Max;i++)
    p->next[i]=NULL;
p->num = 0;
return p;

}

插入字符串

插入操作接受字典树的根节点与字符串。从根节点开始向下将字符串从头到尾一个一个的向下存储。如果这个字符串的前缀在之前并未存储过，则创造结点后直接指向即可。若这个字符串的前缀已经存储在字典树种，则可以将在这个结点的Num+1来代表拥有这个前缀的字符串数量+1

void Insert( char *str,Node* head){
    int len =strlen(str);
    Node *t,*p=head;
    for(int i=0;i<len;i++){
        int c = str[i]-'a';
        if(p->next[c]==NULL){
            t= Creat();
            p->next[c]=t;
            t->num ++;
            p=p->next[c];
        }else
        {
            p=p->next[c];
            p->num++;
        }

    }
}

作用：

至此字典树的构造就已经完成了，那么字典树有什么作用呢？其实从字典树的存储结构来看，他的优点在于处理字符串前缀的问题。

这是一道昨天数据结构的研讨题，将这道题放在查找与散列映射这章我想必然肯定是用某种数据结构方式来达到快速查询的目的，于是很自然的想到了使用字典树。用字典树存储所有的单词，那么我们在查询前缀的时候，只需要将前缀从根节点往下爬到前缀终点时返回当前的num值即可。

查询函数

int Search(char* str, Node* head){
    Node *p =head;
    int len =strlen(str);
    int count = 0;
    for(int i=0;i<len;i++){
        int c = str[i]-'a';
        if(p->next[c]==NULL){
            return 0;
        }
        else{
            p=p->next[c];
            count = p->num;
        }
    }

    return  count ;

}

总结：

至此字典树的就已经讲完啦，字典树的优点与应用十分明显，事实上也有很多关于字符串的算法用到了字典树这一结构，不过这就以后再说了。