平衡二叉树详解

2016-05-03

概述：

正好上礼拜数据结构讲完了平衡二叉树，不过由于老师的模板实在是看的我头晕，就决定自己动手丰衣足食。自己写一个平衡二叉树的模板。本文将主要介绍平衡二叉树的构造，删除，以及自调整。顺便一提，本来打算周末写完的，然而百度第一条平衡二叉树的参考资料代码完全是有错误的。。。坑死我了

定义：

平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

第一步：结点信息

class Node{
private:
    Node* lson;//左儿子地址
    Node* rson;//右儿子地址
    int height;//结点高度
    int data;//节点存储数据，这里为了方便我直接用int代替模板
    Node* par;//父亲指针
    friend class AVL;//友元类AVL
public:
    Node(int Data,Node* Par):
    lson(NULL),rson(NULL),data(Data),height(0)
    ,par(Par){};
};

第二步：平衡二叉树声明

class AVL{

private:
    Node* root; //二叉树根
    int GetHeight(Node* node); //辅助函数
    void Rotate_LL(Node* node); //左单旋
    void Rotate_RR(Node* node); //右单旋
    void Rotate_LR(Node* node); //左右旋转
    void Rotate_RL(Node* node); //右左旋转
    void insert(Node* &node,int Data,Node* Par); //内调插入
    void trans(Node* node); //内调中序遍历
    void del(Node* &node,int data); //内调删除
    bool isleft(Node* par); //辅助函数
public:
    Node* GetRoot(){
        return root;
    }
    AVL():root(NULL){};
    void Insert(int Data); //插入接口
    void Trans(); //中序遍历接口
    void CCTrans(); //层次遍历
    void Delete(int Data); // 删除接口
};

两个辅助函数

第一个辅助函数返回所输入的结点的树高，空树为-1，根节点为0，否则则为两个儿子树高最大值+1。第二个辅助函数则是为了确定输入结点是他的父亲节点的左儿子还是右儿子，左儿子则输出1，否则输出0.（使用这个辅助函数前必须先判断这个结点的父亲节点是否为NULL）

int AVL::GetHeight(Node* node){
    if(node!=NULL)
        return node->height;
    return -1;
}

bool AVL::isleft(Node* node){
    Node* Par = node->par;
    if(Par->lson==node)
        return true;
    else
        return false;
}

第三步：旋转

对于一个平衡的节点，由于任意节点最多有两个儿子，因此高度不平衡时，此节点的两颗子树的高度差2.容易看出，这种不平衡出现在下面四种情况：

　　1、6节点的左子树3节点高度比右子树7节点大2，左子树3节点的左子树1节点高度大于右子树4节点，这种情况成为左左。

　　2、6节点的左子树2节点高度比右子树7节点大2，左子树2节点的左子树1节点高度小于右子树4节点，这种情况成为左右。

　　3、2节点的左子树1节点高度比右子树5节点小2，右子树5节点的左子树3节点高度大于右子树6节点，这种情况成为右左。

　　4、2节点的左子树1节点高度比右子树4节点小2，右子树4节点的左子树3节点高度小于右子树6节点，这种情况成为右右。

　　从图2中可以可以看出，1和4两种情况是对称的，这两种情况的旋转算法是一致的，只需要经过一次旋转就可以达到目标，我们称之为单旋转。2和3两种情况也是对称的，这两种情况的旋转算法也是一致的，需要进行两次旋转，我们称之为双旋转。

单旋转

单旋转是针对于左左和右右这两种情况的解决方案，这两种情况是对称的，只要解决了左左这种情况，右右就很好办了。图3是左左情况的解决方案，节点k2不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的左子树X子树，所以属于左左情况。

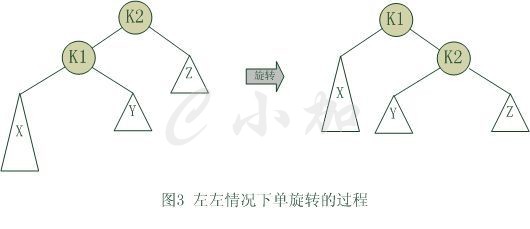
为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质.

　　这样的操作只需要一部分指针改变，结果我们得到另外一颗二叉查找树，它是一棵AVL树，因为X向上一移动了一层，Y还停留在原来的层面上，Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同，插入操作使得X高度长高了。因此，由于这颗子树高度没有变化，所以通往根节点的路径就不需要继续旋转了.

代码如下：

//左单旋
void AVL::Rotate_LL(Node* k2){
    Node* Par= k2->par;
    Node* k1 = k2->lson;
    //注意将k1的右子树转接到k2的左子树下，必须注意再用Par连接起来
    //否则会让树断裂
    k2 ->lson = k1->rson;
    if(k1->rson!=NULL)
    k1 ->rson ->par = k2;

    k1->rson = k2;
    k2->par = k1;

    k1->par = Par;
    if(Par!=NULL){
    int Isleft =-1;
    if(Par->lson==k2){
        Isleft=1;
    }
    else
        Isleft=0;
    if(Isleft){
        Par->lson = k1;
    }
    else
        Par->rson = k1;
    }
    else{
        root = k1;
    }
    k2->height = max(GetHeight(k2->lson),GetHeight(k2->rson))+1;
    k1->height = max(GetHeight(k1->lson),GetHeight(k1->rson))+1;
}

右单旋：

void AVL::Rotate_RR(Node* k2){
    Node* Par =k2->par;
    Node* k1 = k2->rson;

    k2 ->rson = k1->lson;
    if(k1->lson!=NULL)
    k1->lson->par = k2;

    k1->lson = k2;
    k2->par = k1;
    k1->par = Par;

    int Isleft =-1;
    if(Par!=NULL)
    {
        if(Par->lson==k2){
            Isleft=1;
        }
        else
        Isleft=0;

        if(Isleft){
            Par->lson = k1;
        }
        else
            Par->rson = k1;
    }
    else{
        root = k1;
    }

    k2->height = max(GetHeight(k2->lson),GetHeight(k2->rson))+1;
    k1->height = max(GetHeight(k1->lson),GetHeight(k1->rson))+1;
}

双旋转

　　对于左右和右左这两种情况，单旋转不能使它达到一个平衡状态，要经过两次旋转。双旋转是针对于这两种情况的解决方案，同样的，这样两种情况也是对称的，只要解决了左右这种情况，右左就很好办了。图4是左右情况的解决方案，节点k3不满足平衡特性，因为它的左子树k1比右子树Z深2层，而且k1子树中，更深的一层的是k1的右子树k2子树，所以属于左右情况.

为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树.

//左右双旋
void AVL::Rotate_LR(Node* node){
    Rotate_RR(node->lson);
    Rotate_LL(node);
}
//右左双旋
void AVL::Rotate_RL(Node* node){
    Rotate_LL(node->rson);
    Rotate_RR(node);
}

第四步：插入

插入的方法和二叉查找树基本一样，区别是，插入完成后需要从插入的节点开始维护一个到根节点的路径，每经过一个节点都要维持树的平衡。维持树的平衡要根据高度差的特点选择不同的旋转算法

void AVL::insert(Node* &node,int Data,Node* Par){

    if(node==NULL){
        node = new Node(Data,Par);
        return;
    }
    if(Data<node->data)
    //如果DATA小于节点的值,就继续在节点的左子树中插入DATA
    {
        insert(node->lson,Data,node);
        if(GetHeight(node->lson)-GetHeight(node->rson)==2){
            if(Data<node->lson->data){
                Rotate_LL(node);
            }
            else{
                Rotate_LR(node);
            }
        }
    }
    else
    //则DATA大于结点值，往结点的右子树插入DATA
    {
        insert(node->rson,Data,node);
        if(GetHeight(node->rson)-GetHeight(node->lson)==2){
            if(Data>node->rson->data){
                Rotate_RR(node);
            }
            else{
                Rotate_RL(node);
            }
        }  
    }
    node->height = 
    max(GetHeight(node->lson),GetHeight(node->rson))+1;
}

//插入接口
void AVL::Insert(int Data){
    insert(root,Data,NULL);
}

注：很多教材上（包括我自己的教材）在讲到插入结点后通过旋转来自调整时，通常都会引入一个平衡因子BF，其值为右子树树高减去左子树树高，然后通过在查找的过程中，记录平衡因子的数值，然后根据平衡因子的变化关系来决定旋转类型，而我这里则是根据插入值前往的左右子树情况来决定。假设插入值大于当前结点值，那么将插入值向结点值的右子树插入时，必然是当前结点的右子树的树高可能被增加，那么也就是说旋转的类型要么是右单旋，要么是右左双旋，反之亦然。

　　所以我们可以通过递归的方式，先将子树的树高求出后再求当前结点的树高，然后再来判断是否需要旋转。

第五步：删除

删除的方法也和二叉查找树的一致，区别是，删除完成后，需要从删除节点的父亲开始向上维护树的平衡一直到根节点。

//删除接口
void AVL::Delete(int Data){
    del(root,Data);
}
//内调删除
void AVL::del(Node* &node,int Data){
    if(node==NULL){
        return;
    }
    if(Data<node->data)
    //Data小于结点值，往左子树搜索
    {
        del(node->lson,Data);
        if(GetHeight(node->rson)-GetHeight(node->lson)==2){
            if(node->rson->lson!=NULL&&(GetHeight(node->rson->lson)>GetHeight(node->rson->rson)) )
                Rotate_RL(node);
            else
                Rotate_RR(node);
        }
    }
    else if(Data>node->data)
    //Data大于节点值，往右子树搜索
    {
        del(node->rson,Data);
        if(GetHeight(node->lson)-GetHeight(node->rson)==2){
            if(node->lson->rson!=NULL&& (GetHeight(node->lson->rson)>GetHeight(node->lson->lson) ))
                Rotate_LR(node);
            else
                Rotate_LL(node);
        }
    }
    else if(node->data==Data){

        if(node->lson!=NULL&&node->rson!=NULL)
        //左右子树都存在
        {
            Node* tmp = node->rson; //指向结点的右儿子
            Node* Par = node->par;
            int IsL = isleft(node);
            while(tmp->lson!=NULL) tmp =tmp->lson; //得到结点的直接后继
            node->data = tmp->data;//将值赋值给当前结点
            if(Par!=NULL)
            {
            if(IsL)
                Par->lson = node;
            else
                Par->rson = node;
            }
            else{
                root = node;
            }
            del(node->rson,tmp->data); //删除直接后继的值得结点
            if(2==GetHeight(node->lson)-GetHeight(node->rson))
            {
                if(node->lson->rson!=NULL&& (
                GetHeight(node->lson->rson)
                >GetHeight(node->lson->lson)))
                    Rotate_LR(node);
                else
                    Rotate_LL(node);
            }
        }
        else
        //只存在一个子树或不存在子树
        {
            Node* Par =node->par;
            Node* tmp =node;
            int IsL = -1;
            if(node->lson==NULL&&node->rson!=NULL){
                if(Par!=NULL){
                     IsL = isleft(node);
                }
                node = node->rson;
                node ->par = Par;
                if(Par!=NULL){
                    if(IsL)
                        Par->lson = node;
                    else
                        Par->rson = node;
                }
                else{
                    root = node;
                }
            }
            else if(node->lson!=NULL&&node->rson==NULL){
                if(Par!=NULL){
                    IsL = isleft(node);
                }
                node = node->lson;
                node ->par = Par;
                if(Par!=NULL){
                    if(IsL)
                        Par->lson = node;
                    else
                        Par->rson = node;
                }
                else{
                    root = node;
                }
            }
            else if(node->lson==NULL&&node->rson==NULL){
                if(Par!=NULL){
                    IsL = isleft(node);
                    if(IsL)
                        Par->lson=NULL;
                    else
                        Par->rson=NULL;
                }
                else{
                    root = NULL;
                }
            }
            delete(tmp);
        }
    }
    if(node==NULL) return;
    //递归得到当前结点树高
    node->height=max(GetHeight(node->lson),GetHeight(node->rson))+1;
    return;
}

第六步：遍历,测试。

我将当初放在了链接上，需要的可以自取，若发现错误，请联系我，我将及时改正。

第七步：关于效率

此数据结构插入、查找和删除的时间复杂度均为O(logN)，但是插入和删除需要额外的旋转算法需要的时间，有时旋转过多也会影响效率。

　　关于递归和非递归。我用的是递归的方法进行插入，查找和删除，而非递归的方法一般来说要比递归的方法快很多，但是我感觉非递归的方法写出来会比较困难，所以我还是选择了递归的方法。

概述：

定义：

第一步：结点信息

第二步：平衡二叉树声明

第三步： 旋转

第四步： 插入

第五步： 删除

第六步： 遍历,测试。

第七步： 关于效率

第三步：旋转

第四步：插入

第五步：删除

第六步：遍历,测试。

第七步：关于效率