Splay Tree(伸展树)
是BBST家族中一种很“潇洒”的数据结构,实际上,它在很多情况下整体上并不处于“平衡状态”,即不能保证对所有节点的访问控制在O(logn)。但是它的设计很有现实意义,(它的设计理念十分符合“以经常性时间为重点”和“局部性原理”这两条系统结构设计的定量原理)。
顺便一提,JAV没有指针真是太棒了。
设计思路
对于传统的平衡搜索树如AVL树,它假定每次对每个节点的访问是等概率的,所以每次动态操作后都“小心翼翼”地维护着平衡因子,从而使得最深的节点的访问成本也能控制在O(logn)。而现实情况中对数据的访问通常并不是等概率的,相反,它常具有局部性;在关注吞吐率而不是单次操作的场合,这一问题更为突出。
这里我们转而关注连续访问一批数据的总体时间。要想总体时间少,我们采用贪心策略,让越经常被访问的节点访问成本越小,这一点和哈夫曼编码的设计如出一辙;然而此处的每个节点的“经常性”是动态变化的,可以有一部分历史数据作为“经验”,但通常要把每次访问的情况吸收到经验中作为下次调整的参考。
由此得出Splay Tree的设计思路:按照“经常性”动态调整拓扑结构,一种实现方法就是:每次把刚刚访问过的节点调整到树根。
Splay操作
作为平衡树,Splay树也是通过左旋和右旋来自调整树的结构
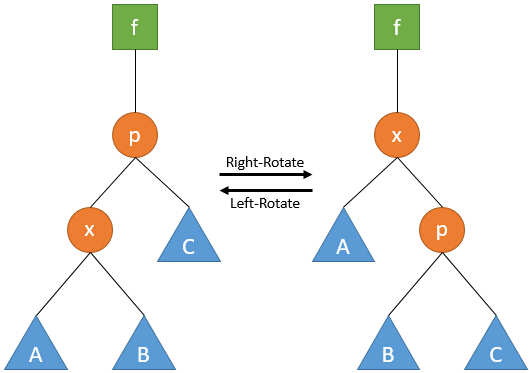
关于旋转操作,在我的平衡树操作有提.
Splay树上有两个基本的调整操作:
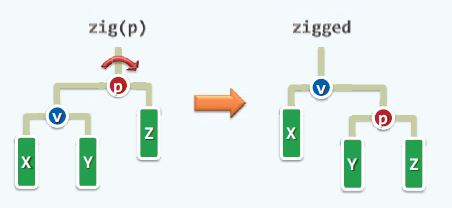
zig
zag
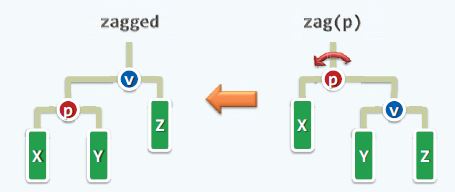
这样的zig/zag局部拓扑结构调整,在实现步骤上可以分如下三步走.
- v与p的祖先g建立连接
- v的孩子Y过继给p
- v与p角色互换
在基本操作的基础上,Splay有三种操作
zig
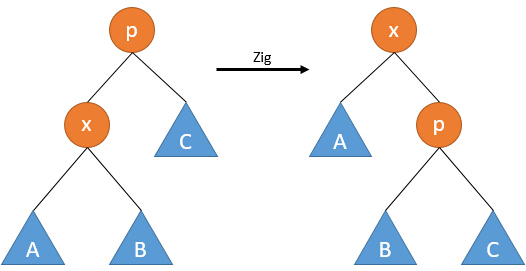
直接根据x节点的位置,进行左旋或右旋。
该操作将x节点提升了一层。
- Zig-Zig
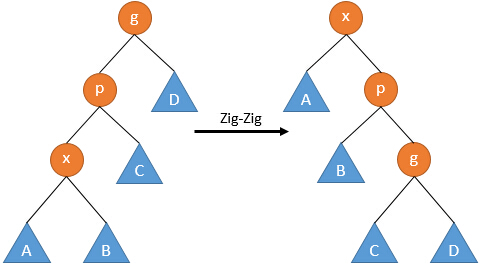
若p不是根节点,还有父亲节点g,且p和x同为左儿子或右儿子,则进行Zig-Zig操作:
当x,p同为左儿子时,依次将p和x右旋;
当x,p同为右儿子时,依次将p和x左旋。
注意此处不是将x连续Zig两次。该操作将x节点提升了两层。
Zig-Zag
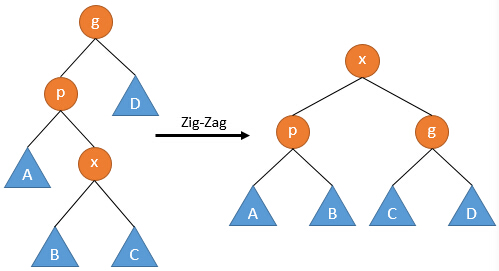
若p不是根节点,则p还有父亲节点g。且p和x不同为左儿子或右儿子,则进行Zig-Zag操作:
当p为左儿子,x为右儿子时,将x节点先左旋再右旋;
当p为右儿子,x为左儿子时,将x节点先右旋再左旋。
该操作将x节点提升了两层。
Splay操作
进一步在Zig,Zig-Zig和Zig-Zag操作上,Splay树定义了”Splay”操作。
对于x以及x的祖先y,splay(x, y),表示对x节点进行调整,使得x是y的儿子节点。
在执行这个操作的时候,需要保证y节点一定是x节点祖先。
值得一提的是,大多数情况下我们希望通过splay操作将x旋转至整棵树的根节点。此时只需令y=NULL即可实现。
Splay树
Splay树的插入和查询操作和普通的二叉搜索树没有什么大的区别,需要注意的是每次插入和查询结束后,需要对访问节点做一次Splay操作,将其旋转至根
insert(key):
node = bst_insert(key) // 同普通的BST插入, node为当前插入的新节点
splay(node, NULL)
find(key):
node = bst_find(key) // 同普通的BST查找, node为查找到的节点
splay(node, NULL)
同时由于Splay的特性,我们还有两个特殊的查询操作。在树中查找指定数key的前一个数和后一个数。
我们先将key旋转至根,那么key的前一个数一定是根节点左儿子的最右子孙,同时key的后一个数一定是根节点右儿子的最左子孙。
findPrev(key):
splay( find(key), NULL )
node = root.left
While (node.right)
node = node.right
Return node
findNext(key):
splay( find(key), NULL )
node = root.right
While (node.left)
node = node.left
Return node
splay中的删除key操作:
splay的删除可以采用和一般二叉搜索树相同的方法:即先找到节点key,若key没有儿子则直接删去;若key有1个儿子,则用儿子替换掉x;若key有2个儿子,则通过找到其前(或后)一个节点来替换掉它,最后将该节点Splay到根。
同时,这里还有另一种方法来完成删除操作:
首先我们查找到key的前一个数prev和后一个数next。将prev旋转至根,再将next旋转为prev的儿子。
此时key节点一定是next的左儿子。那么直接将next的左儿子节点删去即可。
delete(key):
prev = findPrev(key)
next = findNext(key)
splay(prev, NULL)
splay(next, prev)
next.left = NULL
值得注意的是: 当key是数中最大或者最小的时候,这样做的会产生错误。为了解决这种情况,一个简单的处理方法是事先在树中增加一个超级大的数和超级小的数来作为头尾。
删除区间
假如要删除一个区间[a,b]的数该怎么做?
因为要删除[a,b],那么我就要想办法把[a,b]的数旋转到一个子树上,再将这个子树删掉就行了。方法和删除一个数相同,首先将a的前一个数prev和b的后一个数next找出来。同样将prev旋转至根,再将next旋转为prev的儿子。那么此时next的左子树一定就是所有[a,b]之间的数了。
deleteInterval(a, b):
prev = findPrev(a)
next = findNext(b)
splay(prev, NULL)
splay(next, prev)
next.left = NULL
值得注意的是: 假如a和b不在树中的话,那么我们可以事先添加a,b两个数,然后再删除区间。
代码(java) hiho 第104周
import java.util.*;
import java.util.Scanner;
public class Main{
static int MIN_K = 0;
static int MAX_K = 1000000005;
public static void main(String[] args) {
Splay mySplay = new Splay(MIN_K);
mySplay.insert(mySplay.root, MAX_K);
Scanner in = new Scanner(System.in);
int n = in.nextInt();
String c;
int k, a, b;
for(int i=0; i<n; i++){
c = in.next();
if(c.equals("I")){
k = in.nextInt();
mySplay.insert(mySplay.root, k);
}
else if(c.equals("Q")){
k = in.nextInt();
Node t = mySplay.search(mySplay.root, k);
if( k < t.k )
t = mySplay.prev(k);
System.out.println(t.k);
}
else if(c.equals("D")){
a = in.nextInt();
b = in.nextInt();
mySplay.deleteInterval(a, b);
}
}
}
}
class Splay {
Node root;
Node _hot;
Splay(){
root = _hot = null;
}
Splay(int k){
root = new Node(k, null);
_hot = root;
}
void zig(Node cur){
if(cur == null) return ;
Node v = cur.l;
if(v == null) return ;
Node g = cur.p;
v.p = g;
if(g != null){
if(cur == g.l) g.l = v;
else g.r = v;
}
cur.l = v.r;
if(cur.l != null) cur.l.p = cur;
cur.p = v;
v.r = cur;
if(cur == root) root = v;
}
void zag(Node cur){
if(cur == null) return ;
Node v = cur.r;
if(v == null) return ;
Node g = cur.p;
v.p = g;
if(g != null){
if(cur == g.l) g.l = v;
else g.r = v;
}
cur.r = v.l;
if(cur.r != null) cur.r.p = cur;
cur.p = v;
v.l = cur;
if(cur == root) root = v;
}
void splay(Node x, Node f){
if(x == null) return ;
while(x.p != f){
Node p = x.p;
if(p == null) return ;
if(p.p == f){
if(x == p.l){
zig(p);
}
else{
zag(p);
}
}else{
Node g = p.p;
if(g == null) return ;
if(g.l == p){
if(p.l == x){
zig(g); zig(p);
}else{
zag(p); zig(g);
}
}else{
if(p.l == x){
zig(p); zag(g);
}else{
zag(g); zag(p);
}
}
}
}
}
Node search(Node cur, int k){
if(cur == null) return _hot;
if(cur.k == k){
splay(cur, null);
return cur;
}
_hot = cur;
if(k < cur.k) return search(cur.l, k);
else return search(cur.r, k);
}
Node insert(Node cur, int k){
if(cur == null){
cur = new Node(k, _hot);
if(k < _hot.k) _hot.l = cur;
else _hot.r = cur;
_hot = cur;
//System.out.println("find place");
splay(cur, null);
//System.out.println(cur.k + "created");
return cur;
}
_hot = cur;
if(k < cur.k) return insert(cur.l, k);
else return insert(cur.r, k);
}
Node prev(int k){
splay(search(root, k), null);
Node cur = root.l;
if(cur == null) return null;
while(cur.r != null) cur = cur.r;
return cur;
}
Node succ(int k){
splay(search(root, k), null);
Node cur = root.r;
if(cur == null) return null;
while(cur.l != null) cur = cur.l;
return cur;
}
void deleteInterval(int a, int b){
Node pa = search(root, a);
if(pa.k != a) pa = insert(pa, a);
Node pb = search(root, b);
if(pb.k != b) pb = insert(pb, b);
Node p = prev(a);
Node s = succ(b);
splay(p, null);
splay(s, p);
Node q = s.l;
_hot = s;
s.l = null;
}
}
class Node{
int k;
Node l, r;
Node p;
Node(){p = null;}
Node(int kk, Node pp){
k = kk;
p = pp;
l = r = null;
}
}
